poptart wrote:Jay said, "The surface of the lake, in perfectly calm conditions, given those parameters, is of course flat."
And this... "Now then, expand that distance out, say for 1,000 miles, such as a typical stretch of sea or ocean, then the surface, to the naked eye, will "appear" flat. It isn't of course, due to gravitational pull."
We're not talking about water molecules bending, and the term bend is just a synonym for curve in this discussion.
Jay said that ocean water curves (or bends) but a 1 mile long lake does not.
I have no idea what his rational is for this incredible take, but that's what he's said.
Completely out of context poptart. I said, perhaps poorly, that the surface of said lake "seems" to be flat. I have repeated this over and over. 88 hit all of the salient points of your three questions perfectly, so no need to repeat those answers here. All water is subject to the laws of gravitational force, etc. that 88 mentioned. It's simple physics.
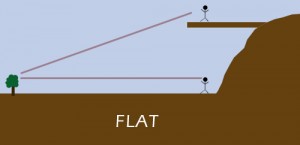
Now then, another example that has been covered before is line of sight, as well as what a viewpoint is like the higher you ascend. Standing in a flat plateau, you look ahead of you towards the horizon. You strain your eyes, then take out your favorite binoculars and stare through them, as far as your eyes (with the help of the binocular lenses) can see.
Then, you climb up the closest hill – the higher the better. You then look again, strain your eyes, stare through the binoculars out to the horizon.
The higher up you are the farther you will see. Usually, we tend to relate this to Earthly obstacles, like the fact we have houses, trees or hills obstructing our vision on the ground, and climbing upwards we have a clear view, but that’s not the true reason. Even if you would have a completely clear plateau with no obstacles between you and the horizon, you would see much farther from greater height than you would on the ground.
This phenomena is caused by the curvature of the Earth as well, and would not happen if the Earth was flat:

Also covered were the varying star constellations. An observation was originally made by Aristotle (384-322 BCE), who declared the Earth was round judging from the different constellations one sees while moving away from the equator.
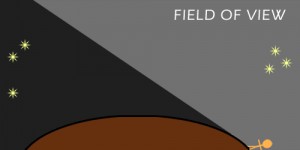
After returning from a trip to Egypt, Aristotle noted that “there are stars seen in Egypt and [...] Cyprus which are not seen in the northerly regions.” This phenomenon can only be explained with a round surface, and Aristotle continued and claimed that the sphere of the Earth is “of no great size, for otherwise the effect of so slight a change of place would not be quickly apparent.”
The farther you go from the equator, the farther the ‘known’ constellations go towards the horizon, and are replaced by different stars. This would not have happened if the world was flat:

There is also the matter of time zones.
If the time in New York is 12:00pm, the sun would be in the middle of the sky. In Beijing, it’s 12:00am, midnight, and the sun is nowhere to be found.
In Adelaide, Australia, it is 1:30am. More than 13 hours ahead. There, the sunset is long gone – so much so, that it’s soon going to rise up again in the beginning of a new day.
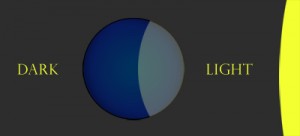
This can only be explained if the world is round, and rotating around its own axis. At a certain point when the sun is shining on one part of the Earth, the opposite side is dark, and vise versa. That allows for time differences and time zones, specifically ones that are larger than 12 hours.
Another point concerning time zones, the sun and flat/spherical Earth: If the sun was a “spotlight” (very directionaly located so that light only shines on a specific location) and the world was flat, we would have seen the sun even if it didn’t shine on top of us (as you can see in the drawing below). The same way you can see the light coming out of a spotlight on a stage in the theater, even though you – the crowd – are in the dark. The only way to create two distinctly separate time zones, where there is complete darkness in one while there’s light in the other, is if the world is spherical.
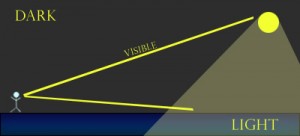
There are other examples to show proof of a round Earth, but you can digest these for a while.








 scientists
scientists







